مقدمه:
با رشد روز افزون وب، سیستمهای پیشنهاد دهنده به کاربران یک چالش بزرگ به حساب میآید. در حالی که کاوش کاربردهای وب نقش عمدهای در پیدا کردن نواحی که برای کاربران جذاب میباشد بر اساس رفتارها و عملیات قبلی کاربر، دارد. این موضوع خصوصا در شبکههای اجتماعی نمود بیشتری پیدا میکند. به عنوان مثال کاربران شبکههای اجتماعی را با استفاده از رفتارها و صفحات و موضوعاتی که اخیراً بازدید کردهاند و هم چنین پروفایلهای آنها میتوان دستهبندی کرده و علاقه مندی آنها را بدست آورد. با استفاده از این علاقه مندیها میتوان صفحات و گروهها و افراد جدیدی را به کاربر شبکهی اجتماعی پیشنهاد داد. کاربران با استفاده از این صفحات با مفاهیم، موضوعات و ... که در این شبکههای اجتماعی وجود داشته و از دید کاربر پنهان بوده یا کاربر برای پیدا کردن آنها می بایست وقت زیادی را تلف کند، آشنا میشود. افراد زیادی در این شبکهها عضو میباشند و پیشنهاد دادن صفحات مورد علاقهی کاربران و افراد مرتبط به آنها میتواند رضایت آنها را بسیار جلب کند. به گونهای که امروزه میتوان گفت یکی از معیارهای مهم برای شبکههای اجتماعی محسوب میشود.
الگوریتمهای فرامکاشفهای
به طور کلی روشها و الگوریتمهای بهینهسازی به دو دسته الگوریتمهای دقیق و الگوریتمهای تقریبی تقسیمبندی میشوند. الگوریتمهای دقیق قادر به یافتن جواب بهینه به صورت دقیق هستند اما در مورد مسائل بهینه سازی سخت کارایی کافی ندارند و زمان اجرای آنها متناسب با ابعاد مسائل به صورت نمایی افزایش مییابد. الگوریتمهای تقریبی قادر به یافتن جوابهای خوب (نزدیک به بهینه) در زمان حل کوتاه برای مسائل بهینهسازی سخت هستند. الگوریتمهای تقریبی نیز به سه دسته الگوریتمهای مکاشفهای و فرامکاشفهای و فوق مکاشفهای بخشبندی میشوند. دو مشکل اصلی الگوریتمهای مکاشفهای، گیر افتادن آنها در نقاط بهینه محلی و همگرایی زودرس به این نقاط است. الگوریتمهای فرامکاشفهای برای حل این مشکلات الگوریتمهای مکاشفهای ارائه شدهاند. در واقع الگوریتمهای فرامکاشفهای، یکی از انواع الگوریتمهای بهینهسازی تقریبی هستند که دارای راهکارهای برون رفت از نقاط بهینه محلی هستند و قابلیت کاربرد در طیف گستردهای از مسائل را دارند. ردههای گوناگونی از این نوع الگوریتم در دهههای اخیر توسعه یافته است. در واقع NP-hard الگوریتمهای فرامکاشفهای برای حل مسایل استفاده میشوند. در این دسته از مسایل که جواب چند جملهای ندارد الگوریتمهای چند جملهای جواب نمیدهد. این مسایل دارای پیچیدگی زمانی بیشتر از چند جملهای میباشند. از آنجایی که مسایل امروزه دارای پیچیدگیهای بیشتری هستند و به دلیل انعطافپذیری و کارایی این الگوریتمها در مقایسه با الگوریتمهای مکاشفهای از این الگوریتمها امروزه بیشتر استفاده میشود.
کارهای مرتبط
برای حل مسالهی پیشبینی لینک تاکنون از الگوریتمهای مختلفی استفاده شده است. به طور کلی میتوان این الگوریتمها را به سه دستهی کلی تقسیم کرد. این روشها عبارتند از: روشهای برپایهی مشابهت، روشهای حداکثر مشابهت و روشهای برپایهی احتمال. در روشهای برپایهی مشابهت به هر زوج گره اندیسی اختصاص داده میشود. این اندیس میزان مشابهت هر دو گره را نشان میدهد. تمامی لینکهای مشاهده نشده بر اساس مشابهت رده بندی میشوند. لینکهای با مشابه بیشتر دارای مقدار بیشتری میباشند. مشابهت گرهها با استفاده از ویزگیهای اصلی گرهها تعریف میشوند. اگر دو گره دارای ویژگیهای مشترک بیشتری باشند یا دارای ساختار توپولوژیکی مشابهی باشند به عنوان گرههای مشابه در نظر گرفته میشوند. کارهای بسیاری از ویژگیهای توپولوژیکی ساختار شبکه برای پیشبینی لینک استفاده میکنند. در روابط کلی بین زوجها به عنوان الگوی لینک در نظر گرفته میشود. این الگوی لینک شامل الگوی تعاملات و ساختار ارتباطی در شبکه میباشد. اندیسهای مشابهت ساختاری در سه دستهی کلی در نظر گرفته میشود. اندیسهای محلی، اندیسهای سراسری و اندیسهای نیمه محلی. اندیسهای محلی از اطلاعات همسایگی گرهها استفاده میکنند. اندیسهای محلی رایچ شامل همسایههای مشترک، اندیس سالتون، اندیس جاکارد، اندیس سورنسن و .. میباشد. اندیسهای سراسری به اطلاعات توپولوژیکال سراسری نیاز دارند. اندیس کاتز، اندیس جنگل ماتریس و ... از اندیسهای سراسری رایچ میباشند. اندیسهای نیمه محلی به اطلاعات توپولوژیکال سراسری نیاز ندارند اما به اطلاعات بیشتری نسبت به اندیسهای محلی نیاز دارند. اندیس مسیر محلی، قدم زدن تصادفی محلی و ... از جمله این اندیسها می باشد. در مقالهای از اندیس قدم زدن محلی استفاده کرده است. در مقالهای دیگر نیز نویسنده از الگوریتمی با مدل موازی نگاشت-کاهش برای گرافهای بزرگ پیچیده استفاده کرده است.
دستهی دوم شامل الگوریتمهای حداکثر مشابهت میباشند. این روشها برخی مدلهای سازماندهی شده از ساختار شبکه را به عنوان پیشفرض در نظر میگیرند، همراه با جزییات قوانین و پارامترهای مشخص. این پارامترهای مشخص از حداکر مشابهت ساختار مشاهده شده بدست می آیند. سپس مشابهت هر لینک مشاهده نشده بر اساس آن قوانین و پارامترها محاسبه میشود. مدلهای سازماندهی رایج شامل مدل ساختاری سلسله مراتبی و مدل بلاکی تصادفی میباشد. در مجموعهای از ویژگیهای ساده به عنوان مدل ساختاری در نظر گرفته میشود که می تواند برای تشخیص لینکهای از بین رفته یا نادیده گرفته شده استفاده شود. مدل سلسله مراتبی دارای دقت بالایی در مواجه با شبکههایی با سطوح مهم سازمانی مانند شبکههای تروریستی و شبکهی زنجیرهی غذایی میباشد. از آن جایی که نیاز به تولید مقادیر زیادی نمونه برای پیشبینی شبکه وجود دارد این مدل نیاز به پیچیدگی محاسباتی بالایی برای شبکههای با مقیاس بزرگ دارد. پیشبینی لینک بر پایهی روش بلاک تصادفی نه تنها لینکهای از دست رفته یا نادیده گرفته شده را میتواند پیش بینی کند بلکه تصحیح خطاها و پیشبینی را نیز در شبکه انجام میدهد. مثلاً خطاهای لینک در شبکه تعاملات پروتئینی. از جنبهی برنامههای کاربردی واقعی مشکل عمدهی روشهای برپایهی حداکثر مشابهت زمان بر بودن زیاد آن میباشد. و در شبکههای برخط بزرگ که اغلب شامل میلیونها گره میباشند نمیتواند بکار گرفته شود.
دستهی سوم الگوریتمها برپایه مدلهای احتمالی میباشد. هدف این روشها برپایهی مدل انتزاعی کردن ساختار شبکهی زیرین از شبکهی مشاهده شده و سپس پیشبینی لینکهای از دست رفته با استفاده از مدل آموخته شده، میباشد. این روشها ابتدا یک مدل شامل مجموعهای از پارامترهای تنظیم شده میسازند و سپس از استراتژی بهینه سازی برای پیدا کردن مقادیر بهینهی پارامترها استفاده میکنند. مدلهای احتمالی یک تابع هدف برای برقراری یک مدل شامل گروهی از پارامترها که میتواند بهترین مناسب دادههای مشاهده شده از شبکهی هدف باشد را بهینه میکنند. سپس احتمال یک لینک بالقوه با استفاده از احتمال شرطی تخمین زده میشود. سه روش اساسی در این دسته وجود دارند که عبارتند از: مدل رابطهای احتمالی، مدل رابطهای موجودیت احتمالی و مدل رابطهای تصادفی. در روشی را برای پیشبینی لینکهای احتمالی و تحلیل مسیر با استفاده از زنجیرههای مارکوف مطرح کرده است. مطالعات بسیاری در پیشبینی لینک در شبکههای اجتماعی با مقیاس بزرگ تمرکز دارد. در چندین پیشبینی کننده برپایهی تحلیل ساختاری شبکههای چند بعدی ارایه شده است. اگر چه این روشها خاص شبکههای با مقیاس بزرگ در نظر گرفته شده است دقت نتایچ به علت محدودیت در زمان محاسبات تضمینکننده نمیباشد. مسائل پیشبینی لینک دیگری بر روی ویژگیهای گرهها تمرکز دارد. بسیاری از شبکههای دنیای واقعی شامل ویژگیهای گره دستهبندی شده میباشند. به عنوان مثال کاربران در گوگل پلاس دارای ویژگیهایی شامل شغل، دانشگاه، آدرس و ... میباشند. دو منبع اطلاعاتی در شبکههایی با ویژگیهای گره در دسترس میباشد: اطلاعات توپولوژیکال و اطلاعات ویژگی. چگونگی استفاده همزمان این دو منبع اطلاعاتی در پیشبینی لینک موضوع مهمی میباشد. یادگیری ارتباطی فاکتوری کردن ماتریس و روشهای برپایهی alignrent برای این نوع شبکهها استفاده شده است اما عیب آنها در موضوع مقیاس پذیری میباشد.
همان گونه که در بالا بیان گردید، تاکنون الگوریتمهای گوناگونی برای حل این مساله ارائه شده است. برخی روشها از الگوریتمهای ساختاری بدون ناظر استفاده میکنند. در برخی روشها از الگوریتمهایی استفاده شده است که مقیاس پذیر نمیباشند. در صورتی که اندازهی گراف افزایش یابد این روشها کارساز نمیباشند. بنابراین برای حل این مساله از الگوریتمهای فرامکاشفهای استفاده شده است. الگوریتمهای فرامکاشفهای گوناگونی مانند الگوریتم جمعیت مورچگان استنفاده شده است. در مقالههایی از این الگوریتم برای حل مساله استفاده کرده است. در این پژوهش سعی بر این است که با استفاده از الگوریتمهای ترکیبی فرامکاشفهای روشی برای حل این مساله ارائه دهیم که دارای دقت خوبی باشد.
الگوریتم فرامکاشفهای پیشنهادی
الگوریتم ارائه شده در این پژوهش الگوریتم memetic میباشد در این روش الگوریتم پایه الگوریتم ژنتیک میباشد و الگوریتم محلی برای بهینهسازی راه حلها درون آن الگوریتم تپه نوردی میباشد. در این پژوهش فرآیند پیشنهاد در دو گام انجام میگردد. در گام اول عملیات فیلتر کردن انجام میشود. در این عملیات گرههایی که احتمال بالاتری برای پیشنهاد شدن دارند را جدا میکند. در نتیجه تعداد کل گرهها در شبکه که میخواهند پردازش شوند کم میشود.
در گام دوم که ترتیب دهی میباشد برخی خصوصیات و معیارهای شباهت را در نظر گرفته و باعث میشود برخی گرهها در بالای لیست نتایچ قرار بگیرند. در گام فیلتر کردن از مفهوم ضرایب کلاسترینگ استفاده شده و تنها همسایگان همسایهی گره را در نظر میگیرد و بقیه را نادیده میگیرد. در واقع تنها گرههایی که با دو گام از گرهی مرکزی قابل دسترسی باشند را در نظر میگیرد. پس از اجرای گام فیلترینگ نوبت به گام ترتیب دهی میرسد. در این گام پس از اجرای الگوریتم برای هر گره با گرهی مرکز یک مقدار بدست میآید. این مقدار عددی در واقع مشخص میکند که نسبت به سایر گرهها این گره چقدر با گرهی مرکزی احتمال لینک شدن شان وجود دارد. برای بدست آوردن این مقدار از میانگین وزن دار بین سه اندیس مستقل استفاده میکند. هر کدام از این اندیسها خصوصیتی از زیر گرافی که تشکیل شده است را مشخص میکند. برای محاسبهی معیارها در این گام از مفهوم دوستان دوست مشترک استفاده شده است. این مفهوم در واقع مفهوم سادهای میباشد اما در پیشبینی لینک در شبکههای اجتماعی به صورت گستردهای مورد استفاده قرار گرفته است. برای محاسبهی معیارهای اول تا سوم از داده ساختارهای زیر استفاده شده است.
فرض کنید Ci مجموعه گره های همسایه ی گره ی Vi میباشند. DC چگالی(تراکم) همسایگی گرهها در مجموعهی D میباشند. Dci که به آن ضریب کلاسترینگ می گوییم به صورت زیر تعریف می شود.

Mij مقدار عنصر ij ماتریس همسایگی میباشد. بنابراین صورت کسر تعداد گرههای همسایهی همسایههای گره مورد نظر میباشد. مخرج کسر نیز تعداد یالهای clique میباشد. Clique یعنی اگر گراف کامل باشد چه تعداد یال خواهیم داشت. در واقع با این معیار میزان چگالی همسایگی گرههای موجود در مجموعهی C مشخص میشود که تحت عنوان ضریب کلاسترینگ نامیده می شود. در ادامه معیارهای اول تا سوم به ترتیب توضیح داده شده است.
1. معیار اول
اندیس اول به همسایه های مشترک اشاره می کند. در واقع در شبکه های اجتماعی همان دوستان مشترک بین گرهی i و j میباشد.

در فرمول بالا گرهی i گرهی مرکزی فرض شده است. در واقع گرهای که در حال حاضر می خواهیم مورد تحلیل قرار داده و دوستانی را به آن پیشنهاد دهیم. گرهی j نیز گرهای است که می خواهیم با گره مرکزی بررسی شود. گرهی j گرهای در بین مجموعه کاندیدایی است که در گام فیلترینگ استخراج شدهاند.
2. معیار دوم
اندیس دوم در واقع چگالی نتایچ اندیس اول می باشد.

این معیار در واقع سطح چسبندگی(بهم مرتبط بودن) بین دوستان مشترک i و j را مشخص میکند. در شبکههای i اجتماعی گروههای کوچکی که توسط دوستان مشترک بین و j شکل میگیرد اگر دارای ارتباطات زیادی با یکدیگر باشند مقدار این پارامتر افزایش مییابد. اگر دارای ارتباطات خوبی با هم نباشند اندیس این مقدار کوچک میباشد.
3. معیار سوم
اندیس سوم در واقع از اندیس دوم مشتق شده است. این اندیس در واقع چگالی گروه شکل گرفته توسط گرههای ni و nj میباشد. در اندیس دوم گرههای مشترک دو گره در نظر گرفته شده است و در این اندیس اجتماع گرههای بین دو گره در نظر گرفته میشود.

پس از محاسبهی این مقادیر، اندیسهای اول تا سوم، نوبت به فاز کالیبراسیون میرسد. در ادامه این فاز توضیح داده خواهد شد.
4. فاز کالیبراسیون
در این فاز سه اندیس با هم ترکیب شده و یک مقدار به عنوان خروجی می دهد. به عنوان ساده ترین راه حل میتوان میانگین وزن داری بین این سه اندیس بدست آورد و به عنوان عدد خروجی در نظر گرفت. در این پژوهش از الگوریتم ممتیک جهت بهینه کردن ضرایب این اندیسها استفاده میشود. تک تک ضرایب اندیسها میبایست بگونهای باشد که در کل این ضریب بهینه باشد. بهینه سازی در این جا به این معنی است که کاربران مهم تر در ابتدای لیست قرار بگیرند. اهمیت کاربر در شبکهی اجتماعی به متن و محتوای شبکه مربوط میشود. بنابراین از یک کاربر به کاربر دیگر ممکن است این اهمیت متفاوت باشد. بنابراین تابع بهینه سازی میبایست ساختار جاری ارتباطات کاربر را نیز مورد بررسی قرار دهد. برای ساخت تابع بهینه سازی میبایست تغییراتی در فاز فیلترینگ اعمال گردد. به این صورت که میبایست گرههایی که کاربر هم اکنون با آنها در ارتباط است نیز مورد بررسی قرار گیرد. برای در نظر گرفتن محتوای کاربر که مختص خود او میباشد تنها راه در نظر گرفتن ساختار ارتباطات کنونی کاربر میباشد. بنابراین در این فاز الگوریتم ممتیک را بر روی دوستان کاربر اعمال میکنیم. پس از اعمال این الگوریتم ضرایب بهینه برای اندیسهای اول تا سوم بدست میآید. تابع بهینه سازی در زیر آورده شده است.
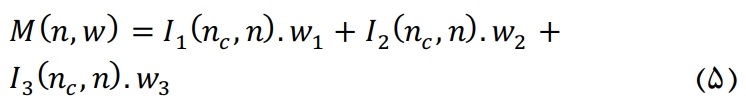
پس از بدست آوردن بهترین ضرایب پارامترها نوبت به اعمال آنها بر روی مجموعهی کاندیدا که خروجی فاز فیلترینگ میباشد میرسد. در زیر الگوریتم ژنتیک و بهینه سازی محلی آن که الگوریتم تپه نوردی میباشد آورده شده است.
5. الگوریتم ژنتیک
برای حل این مساله از الگوریتم ژنتیک دودویی استفاده شده است. الگوریتم ژنتیک ارائه شده برای این مساله در بخشهای زیر به ترتیب توضیح داده شده است.
- کدگذاری مساله: در این الگوریتم برای نمایش مساله از یک ساختار استفاده شده است. هر ساختار در واقع یک فرد در الگوریتم ژنتیک است که یک راه حل برای مساله میباشد. هر ساختار از سه بایت تشکیل شده است. مقدار هر بایت در بازهی بین 0 تا 255 میباشد که همان وزن اندیس موردنظر میباشد. جهت انجام عملگرها اندیسها به صورت بیتی در نظر گرفته میشوند. مقداردهی اولیهی مساله نیز بصورت تصادفی میباشد. در واقع به ازای هر فرد سه عدد در بازهی گفته شده به صورت تصادفی تولید میشود.
- عملگر انتخاب: در این عملگر به تعداد نصف جمعیت و در هر دفعه دو والد بصورت تصادفی انتخاب میشود. عملگر ترکیب بین این دو والد انجام میگیرد.
- عملگر ترکیب: برای این عملگر از روش ترکیب تک نقطهای استفاده شده است. در این عملگر دو والد بصورت تصادفی انتخاب میشوند. سپس یک نقطه به ازای هر اندیس بصورت تصادفی انتخاب میشود. قسمت اول والد اول و قسمت دوم والد دوم فرزند اول را تولید میکنند. قسمت دوم والد اول و قسمت اول والد دوم نیز فرزند دوم را تولید میکنند. این روال برای هر اندیس تکرار میشود. پس از انجام عملیات ترکیب نوبت به عملگر جهش میرسد.
- عملگر جهش: در این عملگر با احتمال ۴ درصد برای هر اندیس جهش انجام میگیرد. برای هر فرزند تولید شده این عملگر انجام میگردد. به ازای هر اندیس با احتمال ۴ درصد جهش خواهیم داشت. از آن جایی که ساختار ضرایب اندیسها به صورت بایتی میباشد و نمایش آنها را نیز به صورت بیتی در نظر میگیریم. به ازای هر بیت اگر جهش انجام گیرد مقدار آن بیت را از صفر به یک یا بالعکس تغییر میدهد. در اصل این عملگر از همگرایی زود رس الگوریتم ژنتیک جلوگیری میکند. سپس نوبت به ارزیابی راه حلهای فرزند میرسد.
- عملگر ارزیابی: عملگر ارزیابی در این الگوریتم همان تابع بهینه سازی میباشد که قبلاً در قسمت کالیبراسیون توضیح داده شد. در واقع ضرایب هر اندیس در مقدار اندیس که به ازای هر کاندید میباشد ضرب شده و میانگین وزن دار آن محاسبه میشود. پس از آن که مقدار ارزیابی هر راه حل محاسبه شد نوبت به انتخاب نسل بعد میرسد. البته قبل از انتخاب نسل بعد، الگوریتم جستجوی تپهنوردی نیز برای بهینه کردن راه حلهای فرزند تولید شده به کار گرفته میشود که در بخش ۴ - ۶ توضیحات آن آورده میشود.
- انتخاب نسل بعد: در این مرحله تعداد راه حلها دو برابر تعداد جمعیت میباشد. در واقع مجموع جمعیت این نسل به اضافهی جمعی فرزندهای تولید شده میباشد. بنابراین برای انتخاب نسل بعد نیاز است که از بین این راه حل تنها به اندازهی جمعیت راه حل انتخاب کنیم. روشهای گوناگونی برای انتخاب نسل بعد وجود دارد. در این مساله از روش بهترین مناسب استفاده میشود. در واقع در این الگوریتم کلیهی راه حلها که شامل راه حلهای اولیه و راه حلهای فرزند میباشند مرتب میشوند. مرتبسازی بصورت نزولی انجام میگردد. سپس به تعداد جمعیت از اول شروع به انتخاب میکنیم. یعنی بهترین راه حلها انتخاب میشوند.
6. الگوریتم جستجوی تپه نوردی
از الگوریتم جستجوی تپه نوردی به منظور جستجوی محلی در حول راه حلهای تولید شده استفاده میشود. در واقع از الگوریتم ژنتیک برای جستجوی فضای مساله استفاده شده و از الگوریتم جستجوی تپه نوردی به منظور جستجوی بیشتر حول راه حلهای پیدا شده استفاده میشود که در واقع میتوان آن را به عنوان الگوریتم جستجوی محلی در نظر گرفت. در این الگوریتم ابتدا تعدادی از فرزندهای ایجاد شده برای جستجو انتخاب میشود. بنابراین از نرخ 0.3 استفاده شده است. یعنی سی درصد فرزندهای تولید شده برای جستجوی بیشتر انتخاب میشود. از آنجایی که این الگوریتم هزینهبر میباشد نمیتوان بر روی همهی راه حلهای فرزند این الگوریتم را اجرا کرد. الگوریتم جستجوی تپه نوردی دارای ایدهی سادهای میباشد. از راه حل اولیهی شروع کرده سپس یک شیب را در نظر میگیرد. با اضافه کردن آن شیب به مقدار اولیه راه حل جدیدی تولید میشود. پس از آن که راه حل جدید تولید شد مقدار ارزیابی برای آن محاسبه میشود. اگر مقدار آن بهتر شده باشد راه حل جدید را به عنوان راه حل جاری در نظر گرفته و به همین صورت ادامه میدهد. این راه حل را تا جایی ادامه میدهد که دیگر راه حل بهتری پیدا نشود. در این پژوهش نیز به ازای هر اندیس این الگوریتم تکرار میشود. ابتدا برای اندیس اول درون راه حل دو اندیس دیگر را ثابت در نظر گرفته و عدد اندیس اول را با مقداری تصادفی جمع میکنیم. البته میبایست چک کنیم که این مقدار از بیشینهی بازه بیرون نزند. سپس با توجه به مقدار اندیس جدید دوباره ارزیابی را انجام میدهیم. اگر بهبودی نسبت به قبل داشته باشیم اندیس جدید جایگزین میشود. در غیر این صورت کاری انجام نمیدهیم و همان مقدار اندیس قبلی باقی میماند. در این الگوریتم اگر تا چهار بار بهبودی حاصل نشد الگوریتم خاتمه مییابد. روال بالا را برای اندیسهای دوم و سوم راه حل نیز تکرار میکنیم. در پایان راه حل فرزند ممکن است دچار تغییراتی شده باشد که جایگزین فرزند قبلی شده است.
فاز پیش پردازش
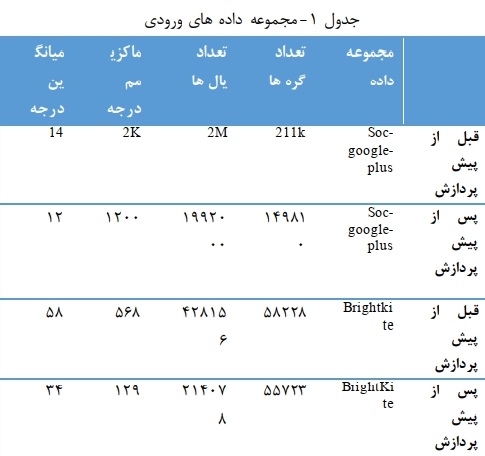
در این فاز ابتدا دادههای ورودی را بررسی کرده و تنها ارتباطات دو طرفه را نگه میداریم. در واقع ارتباطات یک طرفه را حذف میکنیم. تنها پیش پردازش انجام شده بر روی دادهها این مورد میباشد. قبل از انجام این فاز ورودی مساله دارای دویست و یازده هزار گره و دو میلیون یال میباشد. پس از انجام فاز پیش پردازش و حذف ارتباطات یک طرفه ورودی مساله دارای 149810 گره و 1992000 یال میباشد. تعداد گرهها در مجموعهی داده محلی قبل از فاز پیش پردازش 58228 گره و تعداد یالها نیز 428156 یال میباشد. پس از اعمال فاز پیش پردازش تعداد گرهها 55723 و تعداد یالها نیز 214078 میباشد. همان گونه که ملاحظه میشود در مجموعه دادههای محلی تعداد گرهها و یالها پس از انجام پیش پردازش به نسبت کمتری در مقایسه با قبل از پیش پردازش کم شده است. دلیل آن نیز واضح میباشد زیرا در مجموعه دادههای محلی لینکهای بهم متصل ارتباطات قویتری با هم دارند. مجموعه دادههای محلی از مجموعه دادههای دانشگاه استنفورد استخراج شده است که بسیار معتبر میباشد. در جدول 1 مجموعه دادههای سراسری و محلی و تعداد گرهها و یالهای آنها آورده شده است.
پس از اعمال فاز پیش پردازش نوبت به اجرای الگوریتم و محاسبهی اندیسهای اول تا سوم میرسد. از آن جایی که از الگوریتم ممتیک استفاده شده است جه بدست اوردن مقادیر بهینهی پارامترها آزمایشاتی را انجام دادهایم که در ادامه به بررسی آن می پردازیم.
معیارهای ارزیابی
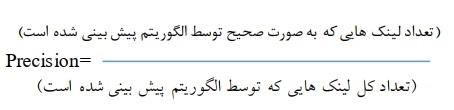
جهت ارزیابی الگوریتم برای حل مسالهی پیشبینی لینک چالشهایی وجود دارد. در واقع به وجود آمدن یک رابطه در شبکهی اجتماعی یا عدم وجود آن تا حدی به کاربر شبکهی اجتماعی بستگی دارد. بنابراین برای تست واقعی الگوریتم نیاز به وجود شبکهی اجتماعی واقعی میباشد. نتایچ الگوریتم را برای هر کاربر اعمال کرده و لیست پیشنهادات را به هر کاربر ارسال کنیم. سپس بر اساس تایید یا رد کاربر کیفیت خروجی الگوریتم مشخص میشود. اما در این مقاله به دلیل عدم دسترسی به شبکهی اجتماعی واقعی از روش ارزیابی متقاطع استفاده شده است. در واقع در این جا از ![]() استفاده شده است.
استفاده شده است.
برای محاسبهی دقت الگوریتم ممتیک نیز خروجی آن که در واقع لیستی از گرهها جهت پیشنهاد میباشد را مقایسه کردهایم. N درصد از ابتدای لیست را در نظر میگیریم. که در این جا n حدوداً 20 انتخاب شده است. یعنی 20 درصد ابتدای لیست پیشنهادی، که مرتب شده میباشد، را مقایسه میکنیم. برای مقایسه نیز پارامتر دقت و بازخوانی در نظر گرفته شده است. یعنی از بین 20% خروجی الگوریتم که لیست پیشنهادی میباشد چند تای آن لینکهای واقعی میباشد که برای آزمایش حذف شده است. فرمول محاسبهی آنها نیز در زیر آمده است.
نتایج الگوریتم ممتیک
جهت بدست آوردن پارامترهای بهینه برای الگوریتم ممتیک آزمایشهایی انجام گرفته شده است و مقادیر بهینهی پارامترها که در نهایت استفاده شده در جدول ۲ آورده شده است.
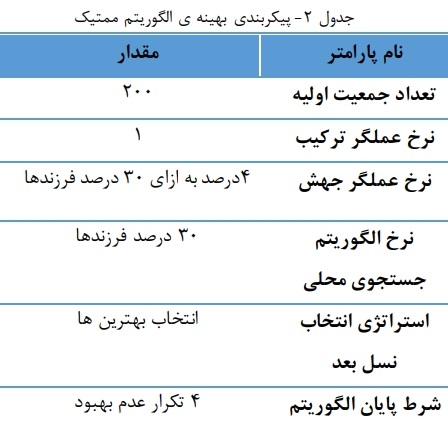
الگوریتم ممتیک را با الگوریتم ژنتیک به ترتیب از لحاظ و دقت در نمودار شکل 1 مقایسه کردهایم.
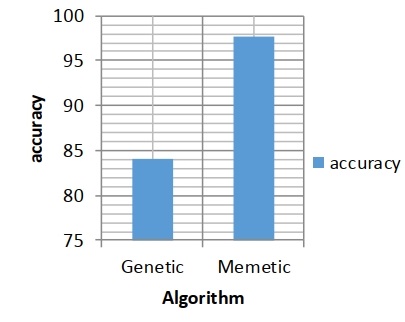
شکل ۱ - نمودار مقایسهی الگوریتم ژنتیک و الگوریتم ممتیک از لحاظ دقت
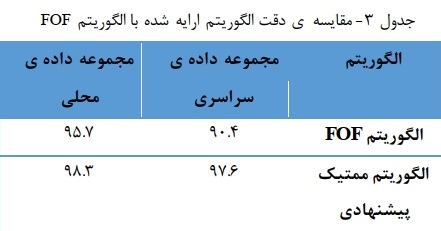
در جدول ۳ الگوریتم ممتیک را با الگوریتم دوستان دوست مقایسه کردهایم. در این الگوریتم لیست کاندیدا دوستان دوست هر گره می باشد.
نتیجهگیری:
در این مقاله از الگوریتم ممتیک برای حل مساله پیشبینی لینک در شبکههای اجتماعی استفاده شد. این مساله کاربردهای فراوانی دارد. مسالهی پیشبینی لینک میتواند در شبکههای مولکولی، شبکههای پیچیده، شبکههای اجتماعی و ... بکار گرفته شود. در حالتی از مسالهی پیشبینی لینک در شبکههای مربوط حوزهی دارو به عنوان راستی آزمایی استفاده میشود. به عنوان مثال الگوریتم اجرا شده و مشخص میکند که این لینکی که به وجود آمده درست بوده یا خیر. در این تحقیق هدف شبکههای اجتماعی میباشد. یعنی در شبکههای اجتماعی به عنوان قلب سیستم پیشنهاد دهنده دوست به افراد استفاده میشود. البته این الگوریتم قابل تعمیم میباشد.
و در آخر:
در این قسمت توضیحاتی آموزنده در مورد پیش بینی و پیشنهاد پیوند در شبکههای اجتماعی با استفاده از الگوریتم فرامکاشفهای ترکیبی ممتیک گذاشته شد. در آینده مطالب بیشتری را در اختیار شما قرار خواهیم داد، با آرزوی بهترینها برای شما خواننده محترم.
منابع:
طاهره جمشیدی، مهدی محرابی، "پیش بینی و پیشنهاد پیوند در شبکههای اجتماعی با استفاده از الگوریتم فرامکاشفهای ترکیبی ممتیک".








دیدگاههای بازدیدکنندگان
در مورد معیار های ارزیابی در داده کاوی مطالبی بگذارید.
558 روز پیش ارسال پاسخ