مقدمه
پیشرفتهای بوجود آمده در جمع آوری داده و قابلیتهای ذخیره سازی در طی دهههای اخیر باعث شده در بسیاری از علوم با حجم بزرگی از اطلاعات روبرو شویم. محققان در زمینههای مختلف مانند مهندسی، ستاره شناسی، زیست شناسی و اقتصاد هر روز با مشاهدات بیشتر و بیشتری روبرو میشوند. در مقایسه با بسترهای دادهای قدیمی و كوچكتر، بسترهای دادهای امروزی چالشهای جدیدی در تحلیل دادهها بوجود آوردهاند. روشهای آماری سنتی به دو دلیل امروزه كارائی خود را از دست دادهاند. علت اول افزایش تعداد مشاهدات (observations) است، و علت دوم كه از اهمیت بالاتری برخوردار است افزایش تعداد متغیرهای مربوط به یك مشاهده میباشد.
تعداد متغیرهایی كه برای هر مشاهده باید اندازهگیری شود ابعاد داده نامیده میشود. عبارت "متغیر" (variable) بیشتر در آمار استفاده میشود در حالی كه در علوم كامپیوتر و یادگیری ماشین بیشتر از عبارات "ویژگی" (feature) و یا "صفت" (attribute) استفاده میگردد.
بسترهای دادهای كه دارای ابعاد زیادی هستند علیرغم فرصتهایی كه به وجود میآورند، چالشهای محاسباتی زیادی را ایجاد میكنند. یكی از مشكلات دادههای با ابعاد زیاد این است كه در بیشتر مواقع تمام ویژگیهای دادهها برای یافتن دانشی كه در دادهها نهفته است مهم و حیاتی نیستند. به همین دلیل در بسیاری از زمینهها كاهش ابعاد داده یكی از مباحث قابل توجه باقی مانده است.
روشهای مبتنی بر استخراج ویژگی
روشهای مبتنی بر استخراج ویژگی، یك فضای چند بعدی را به یك فضای با ابعاد كمتر نگاشت میدهند. این روشها به دو دستهی خطی و غیرخطی تقسیم میشوند. روشهای خطی كه سادهترند و فهم آنها راحتتر است به دنبال یافتن یك زیرفضای تخت عمومی (Global flat subspace) هستند. اما روشهای غیرخطی كه مشكلترند و تحلیل آنها سختتر است به دنبال یافتن یك زیرفضای تخت محلی (Locally flat subspace) میباشند.
از روشهای خطی میتوان به DFT، DWT، PCA و FA اشاره كرد و روشهای دیگر غیرخطی عبارتند از:
- Projection Pursuit (PP): برخلاف روشهای PCA و FA میتواند اطلاعات بالاتر از مرتبهی دوم را تركیب نماید. بنابراین روش مناسبی است برای بسترهای دادهای غیر گاوسی.
- Independent Component Analysis (ICA): این روش نیز یك نگاشت خطی انجام میدهد اما بردارهای این نگاشت لزوماً بر یكدیگر عمود نیستند، در حالی كه در روشهای دیگر مانند PCA این بردارها بر هم عمودند.
- Random Projection (PP): یك روش ساده و در عین حال قدرتمند برای كاهش ابعاد داده است كه از ماتریسهای نگاشت تصادفی برای نگاشت دادهها به یك فضای با ابعاد كمتر استفاده میكند.
از روشهای غیرخطی نیز میتوان به موارد زیر اشاره كرد:
- منحنی های اصلی (Principal Curves)
- خود سازماندهی نقشه ها (Self Organizing Maps)
- کوانتیزاسیون برداری (Vector Quantization)
- الگوریتم های ژنتیک و تکاملی (Genetic and Evolutionary Algorithms)
- رگرسیون (Regression)

تحلیل مولفه های اساسی Principal Component Analysis (PCA)
تکنیک PCA بهترین روش برای کاهش ابعاد داده به صورت خطی میباشد. یعنی با حذف ضرایب کم اهمیت بدست آمده از این تبدیل، اطلاعات از دست رفته نسبت به روشهای دیگر کمتر است. البته کاربرد PCA محدود به کاهش ابعاد داده نمیشود و در زمینههای دیگری مانند شناسایی الگو و تشخیص چهره نیز مورد استفاده قرار میگیرد. در این روش محورهای مختصات جدیدی برای دادهها تعریف شده و دادهها براساس این محورهای مختصات جدید بیان میشوند. اولین محور باید در جهتی قرار گیرد که واریانس دادهها ماکسیمم شود (یعنی در جهتی که پراکندگی دادهها بیشتر است). دومین محور باید عمود بر محور اول به گونهای قرار گیرد که واریانس دادهها ماکسیمم شود. به همین ترتیب محورهای بعدی عمود بر تمامی محورهای قبلی به گونهای قرار میگیرند که دادهها در آن جهت دارای بیشترین پراکندگی باشند. در شکل زیر این مطلب برای دادههای دو بعدی نشان داده شده است.
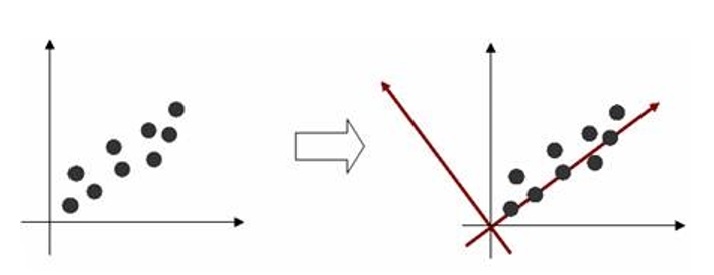
انتخاب محورهای جدید برای دادههای دو بعدی
روش PCA به نامهای دیگری نیز معروف است. مانند:
- Singular Value Decomposition (SVD)
- Karhunen Loeve Transform (KLT)
- Hotelling Transform
- Empirical Orthogonal Function (EOF)
قبل از اینکه به جزئیات این روش بپردازیم ابتدا مفاهیم ریاضی و آماری مرتبط با این روش را بطور مختصر بیان میکنیم. این مفاهیم شامل انحراف از معیار استاندارد، کواریانس، بردارهای ویژه و مقادیر ویژه میباشد.
مفاهیم مقدماتی مورد نیاز در PCA
مفاهیم آماری
فرض کنید X رشتهای از مقادیر است. میانگین این مقادیر از رابطه زیر بدست میآید.
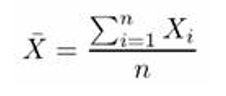
انحراف از معیار نیز از رابطه زیر محاسبه میشود.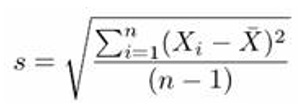
علت اينکه در مخرج رابطه فوق از عبارت n-1 استفاده شده (و نه n) اين است که فرض شده X شامل تمام مقادير موجود نيست بلکه تعدادی از اين مقادير انتخاب شدهاند و در X قرار گرفته اند. يعنی X مجموعه نمونه است و نه کل دادهها. با اين فرض اگر از n-1 در رابطه فوق استفاده شود، انحراف از معيار بدست آمده به انحراف از معيار دادههاي واقعی نزديکتر خواهد بود نسبت به اينکه از n استفاده شود. البته اگر X شامل تمام دادهها باشد آنگاه بايد از n استفاده شود. با بتوان 2 رساندن انحراف از معيار، واريانس بدست میآيد.
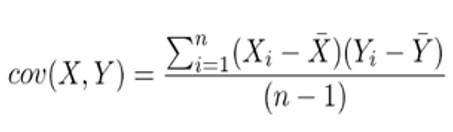
مقداری که از رابطه بالا بدست می آيد در بازه [-1,1] قرار خواهد داشت که يکی از سه حالت زير را بوجود می آورد:
- اگر مقدار بدست آمده مثبت باشد آنگاه X و Y با هم افزايش يا کاهش می يابند.
- اگر مقدار بدست آمده منفي باشد آنگاه با افزايش X مقدار Y کاهش می یابد و بالعکس.
- اگر مقدار بدست آمده صفر باشد آنگاه X و Y از يکديگر مستقلاند.
کوواريانس بين تمامی ابعاد دادهها را ميتوان دو به دو محاسبه کرده و در يک ماتريس ذخيره کرد. به اين ماتريس، ماتريس کوواريانس ميگويند. ماتريس کوواريانس يک ماتريس مربعی متقارن است.
مراحل مختلف الگوریتم PCA
این مراحل در زیر بیان شدهاند:
- انتخاب داده
- کم کردن میانگین از دادهها
- محاسبهی ماتریس کواریانس
- محاسبهی بردارهای ویژه و مقادیر ویژه
- انتخاب مولفهها و ساختن بردار ویژگی
مزایا و معایب PCA
تجزیه و تحلیل مولفههای اساسی یا PCA یک ابزار استاندارد در تجزیه و تحلیل دادههای مدرن در زمینههای مختلف از هوش مصنوعی یا گرافیک کامپیوتری است زیرا این روش ساده و غیرپارامتریک بوده و برای استخراج اطلاعات مربوط به مجموعه دادههایی که پیچیده و گیج کننده هستند، استفاده میشود. با کمترین تلاش، PCA راه حلی را برای چگونگی کاهش ابعاد دادههای پیچیده به ابعاد کمتر برای نشان دادن ساختاری گاه پنهان و ساده که اغلب آن را پایه گذاری میکند، ارائه میدهد.
یکی از زمینههای استفاده از PCA تشخیص الگو و فشردهسازی تصویر است و همچنین این روش برای شناخت و ذخیرهسازی دادههای بیومتریک مناسب است. این روش همانطور که گفته شد روشی برای شناسایی الگوها در دادهها است و دادهها را به گونهای بیان میکند که شباهتها و تفاوتهای آنها با هم منسجم میشوند.
مزیت اصلی PCA، در تعیین اهمیت هر یک از ابعاد برای توصیف متغییری است که از یک مجموعه داده PCA حاصل میشود. همچنین PCA میتواند با استفاده از فشردهسازی دادهها بدون از دست دادن اطلاعات، ابعاد آنها را نیز کاهش دهد. هنگام استفاده از PCA برای تجزیه و تحلیل دادهها، معمولاً میتوان درصد زیادی از واریانس کل را تنها با چند مولفه توضیح داد. مولفههای اصلی طوری انتخاب میشوند که هر یک از آنها یک حداکثر واریانس باقیمانده را توضیح دهد. اولین مولفه اصلی برای توضیح حداکثر نسبت واریانس کل، دومین مولفه برای توضیح حداکثر واریانس باقی مانده و ... انتخاب شدهاند. PCA کاملاً غیرپارامتریک است: در هر مجموعه دادهای که استفاده شود بدون نیاز به گرفتن پارامتر و نادیده گرفتن چگونگی ثبت دادهها، یک پاسخ از آن در خروجی به دست میآید.
ویژگی های روش PCA
ویژگی | تحلیل مولفه های اساسی |
تبعیض بین طبقهبندی ها | روش PCA برای تجزیه و تحلیل اجزای اصلی، تمام دادهها را بدون در نظر گرفتن ساختار کلاس اصلی مدیریت میکند. |
برنامههای کاربردی | برنامههای PCA در زمینههای مهم تحقیقاتی مفید هستند. |
محاسبه برای مجموعه دادههای بزرگ | روش PCA نیازی به محاسبات زیاد ندارد. |
جهت حداکثر تبعیض | جهت حداکثر تبعیض، همانند جهت حداکثر واریانس نیست، زیرا لازم نیست تا از اطلاعات کلاس مانند پراکندگی درون کلاس و بین کلاس استفاده کند. |
متمرکز کردن | روش PCA مسیرهایی که بیشترین تغییرات را دارند، بررسی میکند. |
یادگیری با نظارت | تکنیک PCA یک تکنیک بدون نظارت است. |
| کلاسهای توزیع شده در مجموعههای کوچک | PCA نسبت به روش های دیگر قدرتمند نیست. |
برنامه های مولفه های اساسی
مهم ترین استفاده از PCA، کاهش ابعاد دادهها است. این ابعاد اثر بخشی دادهها را فراهم میکنند. اگر چند مولفهی اول برای اکثر تغییرات در دادههای اصلی انتخاب شوند، بنابراین چند مولفهی اول را میتوان در تجزیه و تحلیل بعدی به جای متغییرهای اصلی استفاده کرد. قرار دادن دادهها با بیش از سه متغییر مشکل میشود. اغلب ممکن است از طریق PCA بسیاری از متغییرهای دادهها توسط دو مولفه اول محاسبه شود و حتی ممکن است مقادیر برای محاسبه دو مولفه طراحی شوند. بنابراین PCA، موجب میشود تا دادهها در دو بعُد طراحی شوند. اغلب استفاده از PCA نشان دهندهی گروهبندی متغییرها است که توسط سایر ابزارها قابل شناسایی نیست.
کاربردهای تحلیل مولفههای اساسی
PCA می تواند در مواردی مورد استفاده قرار گیرد:
- تحقیقات کشاورزی
- زیست شناسی
- هواشناسی
- اقیانوس شناسی
- روانشناسی
- کنترل کیفیت
- بورس (بازار سهام)
محدودیتهای تحلیل مولفههای اساسی
استفاده از تحلیل مولفه های اساسی منوط به فرض هایی است که در نظر گرفته می شود. از جمله:
- فرض خطی بودن (فرض بر اینکه مجموعه داده ترکیب خطی از پایه هایی خاص است.)
- فرض بر اینکه میانگین و کوواریانس از نظر احتمالاتی قابل اتکا هستند.
- فرض بر اینکه واریانس شاخص اصلی داده است.
و در آخر:
در این قسمت توضیحاتی آموزنده در مورد روش تحلیل مولفههای اساسی یا PCA گذاشته شد. در آینده مطالب بیشتری را در اختیار شما قرار خواهیم داد، با آرزوی بهترینها برای شما خواننده محترم.
منابع:
شریفی، علی، (1394)، علم کمومتریکس در شیمی تجزیه و کاهش ابعاد داده ها به روش آنالیز اجزای اصلی PCA، نخستین کنفرانس سراسری دستاورد های نوین در شیمی و مهندسی شیمی، دانشگاه رازی، کرمانشاه.
T. M. V., Suryanareyana, Mistry, P. B., (2016), "Principal component regression for crop yield estimation", Springer birefs in applied sciences and technology, pp 17-25.








دیدگاه خود را بنویسید